Zapis liczb zmiennoprzecinkowych w systemie binarnym

Liczba wymierna to liczba, którą można przedstawić w postaci ułamka zwykłego (licznik i mianownik) np. 1/4, 2/5, 3/10, 1/3.
Mamy również ułamki dziesiętne, np. 0.3, 0.5. Są jednak liczby, których nie da się zapisać w skończonej postaci, np. wynikiem dzielenia 1/3 jest liczba 0.33333(3). W takich przypadkach można zapisać daną liczbę w przybliżeniu z określoną precyzją / dokładnością, np. 0.33 lub 0.333333.

Notacja naukowa / wykładnicza

Liczby można przedstawiać w różnych notacjach, np:
10234.658 to
1.0234658 * 10⁴ w notacji wykładnicznej
1.0234658E+4 w notacji naukowej
Liczbę sprowadza się do takiej postaci, aby część ułamkowa znajdowała się tuż po pierwszej cyfrze znaczącej z przedziału[1, 10). Jest to istotne, ponieważ w systemie binarnym będziemy korzystać z powyższych notacji.

Zamiana ułamków dziesiętnych na liczby binarne

Przy zamianie ułamków na liczby binarne dokonuje się obliczeń w dwóch etapach, osobno część całkowitą, a osobno ułamkową.
Przykład liczby 164.125
Liczba 164 to 1010 0100
Liczba 0.125 to 001
Razem daje to liczbę binarną: 1010 0100.001
W pamięci komputera nie ma jednak kropek. Powyższa liczba musi być zapisana w inny sposób, tylko i wyłącznie za pomocą 0 i 1.

Reprezentacja float

Liczby zmiennoprzecinkowe (float) zapisuje się za pomocą standardu IEEE.754. Możemy posługiwać się liczbami pojedynczej precyzji (float – 32 bity) i podwójnej precyzji (double – 64bity).
Liczby takie zapisywane są za pomocą 3 składowych:
s – 1bit znaku (0 – liczba dodatnia, 1- ujemna)
e – 8 / 11 bitowy wykładnik
Wykładnik może być zapisany na 8 bitach, co daje wartość 256 (bo 2⁸-256). Wykładnik powinien być również ujemny, aby otrzymywać liczby mniejsze od 1, np. 0.00000345. W tym celu koduje się wykładnik dodając do niego wartość 127 lub 1023 dla typu double.
f – 23/52 bitowa mantysa znormalizowana

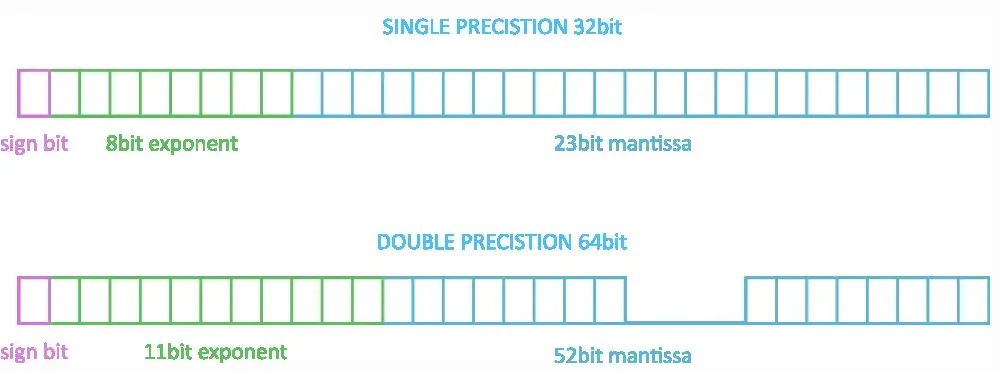
Zapis liczby zmiennoprzecinowej w standardzie IEEE.754

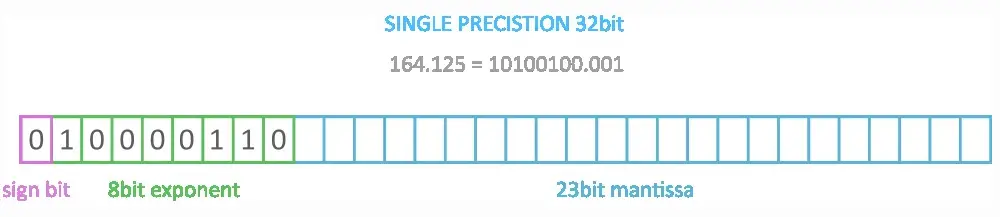
Przykład zapisu liczby 1010 0100.001 (164.125₁₀)
Bit znaku
Liczba jest dodatnia zatem bit znaku wynosi 0.
Wykładnik
Podaną liczbę należy przedstawić w postaci notacji naukowej, przesuwamy separator dziesiętny w lewo o 7 miejsc. Daje to liczbę: 1.0100100001
Przesunięcie nastapiło o 7 miejsc, zatem wykładnik e = 7
Wykładnik należy zwiększyć o 127, co daje wartość 134. Po zamianie na liczbę binarną daje: 1000 0110

Mantysa
Liczba w takiej notacji zawsze będzie miała 1 z przodu. W związku z tym należy się jej pozbyć. Mamy wtedy do czynienia z mantysą znormalizowaną,
z liczby 1.0100100001 powstaje liczba 0100100001
Liczbę należy zapisać na 23 bitach w polu mantysy, wypełniając pozostałe miejsca zerami.

Precyzja liczb zmiennoprzecinkowych

Liczby float i double mają określoną precyzję. 6-7 cyfr dla typu float i 15-16 dla typu double. Skąd się to bierze?
Liczbę zapisuje się na 23 bitach mantysy, 2²³ daje maksymalną wartość 8 388 608, a to właśnie określa precyzję. Dla liczb mniejszych niż 8 388 608 precyzja wynosi 7, ponieważ każda z nich może być zapisana i odczytana. Dla większych liczb precyzja spada do 6, ponieważ wyjdą one poza zakres, a tym samym będą musiały być zaokrąglane do najbliższych liczb, które można zapisać w postaci liczby binarnej.

Czy wszystkie liczby można zapisać w postaci binarnej?

Nie, podobnie jak niektóre liczby dziesiętne, np.1/3 = 0.3(3) nie mogą być zapisane w pełni. Wiele liczb zmiennoprzecinkowych będzie zapisywanych wartościami z pewnym przesunięciem. Tutaj pojawia się słynne równanie: 0.1 + 0.2 != 0.3 co z matematycznego punktu widzenia budzi wzburzenie, bo przecież na kartce 0.1+0.2=0.3 😉
W pamięci komputera 0.1 to nie jest dokładnie 0.1, itd.
Wiedząc o tym, należy pamiętać, by nigdy nie porównywać ze sobą liczb typu float / double. Zawsze należy wziąść pod uwagę margines błędu, który rośnie wraz z tą liczbą.