Systemy liczbowe DEC, BIN i HEX

System dziesiętny

Na co dzień posługujemy się liczbami tworzonymi w systemie dziesiętnym (DEC, Decimal), za pomocą 10 cyfr od 0 – 9.

Jest to system pozycyjny, który posiada rzędy jedności, dziesiątek, setek, tysięcy, itd.… Każdy rząd ma odpowiednią wagę, którą oblicza się za pomocą potęgi liczby 10. Liczba 10 jest podstawą systemu, ponieważ używa się w nim dziesięciu cyfr.

Wykładnik potęgi wynosi 0 dla rzędu jedności i zwiększa się o 1 dla każdego kolejnego rzędu, idąc od prawej strony do lewej.

Rząd jedności jest najmniej znaczący.

Przykłady:

23₁₀ = 2*10¹ + 3*10⁰

145₁₀ = 1*10² + 4*10¹ + 5*10⁰

2034₁₀ = 2*10³ + 0*10² + 3*10¹ + 4*10⁰

System binarny

System dwójkowy (BIN, binarny) tworzony jest z dwóch cyfr 0 i 1 (stąd nazwa). Jest to system pozycyjny, podobnie jak system dziesiętny, z tą różnicą, że wagę rzędu(bitu) oblicza się na podstawie potęgi liczby 2.

11₂ = 1*2¹ + 1*2⁰ = (w systemie dziesiętnym 2 + 1 = 3)

110₂ = 1*2² + 1*2¹ + 0*2⁰ = (w systemie dziesiętnym 4 + 2 + 0 = 6)

00101101₂ = 0*2⁷ + 0*2⁶ + 1*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 32 + 8 + 4 + 1 = 45₁₀

Bit to najmniejsza porcja informacji, która może przyjąć jeden z dwóch stanów, 0 lub 1. W arduino będziemy bardzo często operować na bitach, ale będziemy je grupować i zapisywać w innych jednostkach, np. Bajtach.

1 Bajt składa się z 8 bitów więc może określić 256 różnych konfiguracji – 2⁸ = 256

W programowaniu indeksowanie / liczenie zaczyna się od 0, dlatego za pomocą 1 Bajta można zapisać liczby od 0 do 255.

Liczby binarne można podawać w postaci pełnego bajta 0b/B, np:
0b00101101 lub B00101101

lub kilku bajtów, np. 0011001101010101

1 byte to najmniejsza jednostka informacji, która może być zapisana w pamięci. Chcąc zapisać tylko 1bit w pamięci, system i tak zarezerwuje pełny 1 byte.

System szesnastkowy

System szesnastkowy(HEX, hexadecimal) – system, którego podstawa wynosi 16.

Składa się z cyfr od 0 do 9 i liter od A do F, co daje w sumie 16 znaków:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), F(15)

1A₁₆ = 1*16¹ + 10*16⁰ = 16 + 10 = 26₁₀

B5D₁₆ = 11*16² + 5*16¹ + 13*16⁰ = 2816 + 80 + 13 = 2909₁₀

FF₁₆ = 15*16¹ + 15*16⁰ = 240 + 15 = 255₁₀

Liczby szesnastkowe podaje się za pomocą zapisu 0x, np: 0xA6C

System szesnastkowy jest często używany do adresowania, np. 0x32 oraz określania kolorów RGB z użyciem symbolu hash, np. #FF93A2

Zapis #FF93A2 definiuje kolor na podstawie kanałów RGB:
R: FF₁₆ = 255₁₀
G: 93₁₆ = 147₁₀
B: A2₁₆ = 162₁₀

Dane liczbowe można przedstawić za pomocą różnych systemów. W Arduino najczęściej korzysta się z systemu dwójkowego BIN, dziesiętnego DEC i szesnastkowego HEX. Reprezentacja liczby 45 w 3 systemach liczbowych:

byte num = 0b00101101; //BIN
byte num = 45; //DEC
byte num = 0x2D; //HEX

Zamiana liczb dziesiętnych na binarne i szesnastkowe

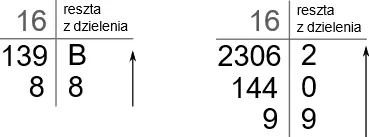
Zamiana liczby dziesiętnej na liczbę w innym systemie polega na jej dzieleniu przez podstawę docelowego systemu (np. 2 lub 16).

Z powstałych reszt dzielenia, tworzy się nową liczbę od dołu w górę.

Zamiana wartości dziesiętnych na binarne:

11₁₀ = 1011₂ (0b1011)    

127₁₀ = 0111 1111₂ (0b01111111)  

Zamiana wartości dziesiętnych na szesnastkowe

139₁₀ = 8B₁₆ (0x8B)                                                                                                       

2306₁₀ = 902₁₆ (0x902)

Zamiana liczb binarnych na szesnastkowe

Zamiana liczb binarnych na szesnastkowe jest bardzo prosta, ponieważ każde 4 bity reprezentują zakres od 0 do 15, czyli dokładnie jeden znak liczby szesnastkowej.

W odwrotny sposób można zamieniać liczby szesnastkowe na binarne.

Zobacz: Operatory binarne